相信很多人都聽過數字濾波器，但是很多人對它都只是淺嘗輒止，并沒有很深入的了解，那么數字濾波器到底什么，它有什么驚為天人的秘密呢！本文將帶你進入它那不一樣的世界。

一、數字濾波器的定義

它可對特定頻率的頻點或該頻點以外的頻率進行有效濾除，是一種對信號有處理作用的器件或者電路。相當于頻率的“篩子"。它輸入輸出均為數字信號，通過一定的運算關系改變輸入信號所含頻率成分的相對比例或者濾除某些頻率成分的器件。

數字濾波器實現的方法的有兩種：一種是使用計算機軟件來實現；另一種方法是使用乘法器，延遲單元和加法器設計一個的數字硬件系統。

二、數字濾波器的定義

數字示波器與模擬示波器相比較，其優勢體現在三點，分別是精度更高、信噪比更高、可靠性更高。

三、數字示波器的分類

數字示波器的種類很多，分類方法也不同。

（1）從功能上分：低通、高通、帶通、帶阻。

（2）從實現方法上分：FIR、IIR.

（3）從設計方法上來分：Butterworth(巴特沃斯)、Chebyshe（切比雪夫）、Ellips （橢圓）等。

（4）從處理信號分：經典濾波器、現代濾波器。

簡單介紹四種典型示波器

本次首先主要介紹經典濾波器中的4種典型濾波器：低通、高通、帶通、帶阻。

1、幅頻特性如下：

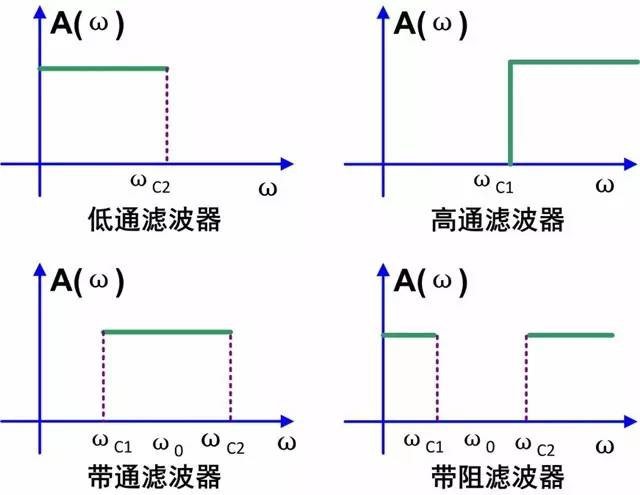
圖1 四種典型濾波器的幅頻特性

2、由上圖1可知，根據頻率特性:

低通濾波器：它允許信號中的低頻或直流分量通過，抑制高頻分量或干擾和噪聲；

通帶0~ωC2，上截止頻率ωC2

高通濾波器：它允許信號中的高頻分量通過，抑制低頻或直流分量；

通帶ωC1~∞，下截止頻率ωC1

帶通濾波器：它允許一定頻段的信號通過，抑制低于或高于該頻段的信號、干擾和噪聲；

通帶ωC1~ωC2，上下截止頻率ωC1、ωC2

中心頻率：ω0=sqrt(ωC1*ωC2)

帶寬：B=ωC1-ωC2

品質因數：Q=ω0/B，反映濾波器的分辨率

帶阻濾波器：它抑制一定頻段內的信號，允許該頻段以外的信號通過。

通帶0~ωC1，ωC2~∞，ω0=sqrt(ωC1*ωC2)

理論上我們知道，低通與高通串聯得帶通濾波器；低通和高通并聯得帶阻濾波器。

四、理想濾波器和實際濾波器的對比

根據圖1四種幅頻特性曲線可知，只有通帶和阻帶，通帶中的增益為常數且信號幅值和相位基本不失真；阻帶中的增益為零，頻率成分衰減為零，通帶與阻帶之間有明顯的分界線，這種為理想濾波器。

理想示波器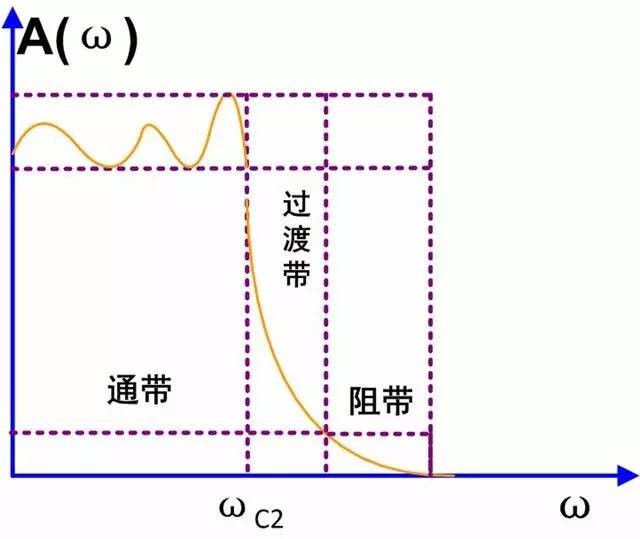

，而通帶阻帶間沒有明顯的界限，兩者之間有一個過度帶。在過渡帶內的頻率成分只會受到不同程度的衰減，不會被*抑制，過渡帶越窄越好也就是通帶外的頻率成分衰減得越快、越多越好，所以ZDS2024示波器新增數字濾波功能，可以使通帶內具有很好的平坦度、阻帶內有足夠的衰減和足夠小的阻帶紋波，以及陡降的過渡帶如下圖3。

圖2 實際低通濾波器的幅頻特性

下圖3為是ZDS2024數字濾波器在設置歸一化截止頻率為0.08的低通巴特沃斯濾波器的幅頻響應曲線：

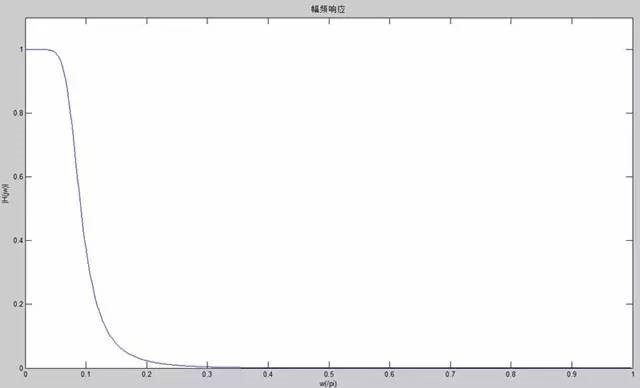
圖3 低通巴特沃斯濾波器的幅頻響應曲線